Global Long-Horizon Planning for Dynamical Systems
One of the lessons from the general public is that rural areas lacked the necessary medical resources to support infected patients, and even urban centers, such as New York City, lacked the infrastructure to handle surges in the disease. Certainly, the military knew of this, as many military missions support humanitarian assistance and disaster relief (HADR). Many HADR missions require the rapid set up and staffing of field hospitals to deliver care to those affected by natural disasters or internal conflicts.
The problem is that these portable medical structures require considerable effort and man-power to assemble, and perhaps not in the best conditions. During the pandemic, it took over three days for volunteers, some of whom contracted Covid during the process, to erect field hospitals. Certainly, in a conflict, personnel assembling a medical facility faces potential dangers. This work focuses on rapid construction of hospital modules to provide advanced healthcare facilities in remote locations. We leverage our prior work on modularity to design hospital sections, or really hospital modules, which can be assembled and reassembled to form different structures. We term these modules as Container Modular Units (CMUs) and these CMUs are specifically designed so they can easily be adapted to multiple use cases, including an Operation Room (OR), an Intensive Care Unit (ICU), a general ward, etc.
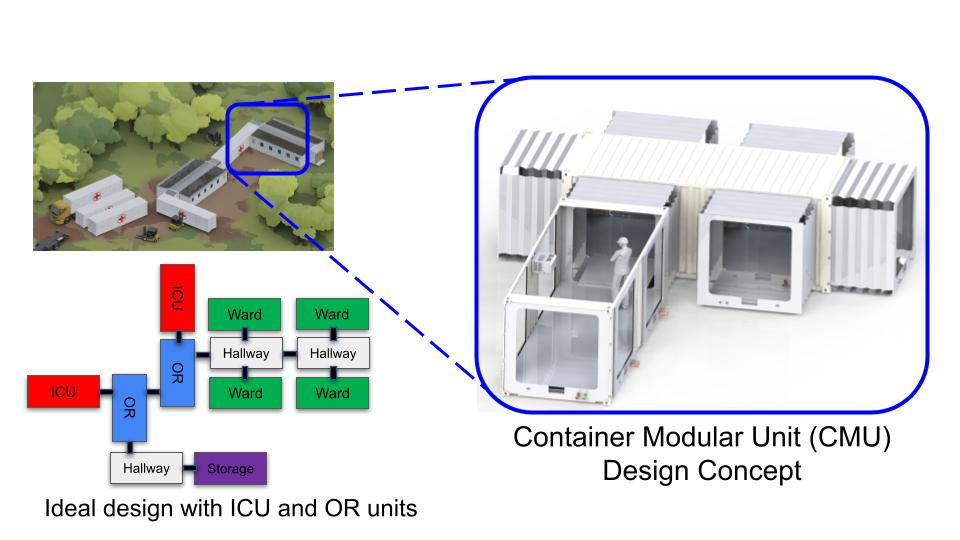
We then utilize our multi-objective optimization algorithms to identify an optimal structure for the hospital modules. Using our state-of-the-art multiagent planning algorithms, we aid hospital construction in a dynamic environment. Finally, the construction of the CMUs is out of scope for this project, we illustrate the efficacy of our approach via simulations in a 3D grid world enviornment.
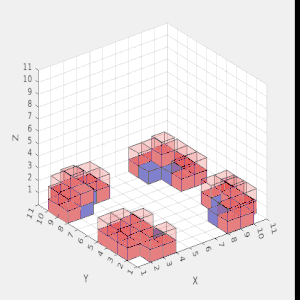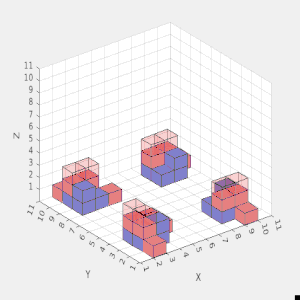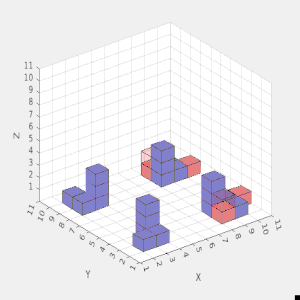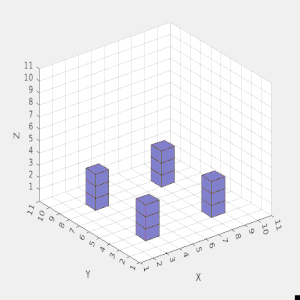
In a Multi-Agent Collective Construction (MACC) problem described above, the intent is to generate a plan for cubic robots to build a three-dimensional structure comprised of cubic blocks. These cubic robots can carry one cubic block at a time; robots may move left, right, forwards, backward, or climb up or down one block. To construct structures taller than one cube, the robots must build supporting scaffolding made of blocks and remove the scaffolding once the structure is built. Prior works sought to create a planner that considered the structure as one monolithic assembly, which becomes intractable for larger workspaces and complex structures. To this end, we present a decomposition algorithm that breaks the structure into substructures that can be planned for independently. We use Mixed Integer Linear Programming (MILP) to plan for each of these substructures and then aggregate the solutions to construct the entire structure. Extensive testing on 200 randomly generated structures shows an order of magnitude improvement in the solution computation time compared to an MILP approach without decomposition. Finally, we leverage the independence between substructures to detect which substructures can be built in parallel.


